В условии дана пирамида с трапецией в основании и двумя противоположными гранями, которые перпендикулярны основанию. Если противоположные грани, перпендикулярные основанию, будут проходить через параллельные стороны трапеции, то две другие боковые грани образуют сверху ребро, пирамида не получится
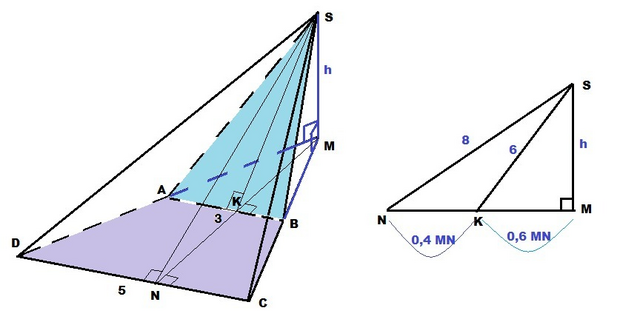
Итак, дана пирамида SABCD, в которой SM - высота;
АВ ║СD; AB = 3; CD = 5; (SAD)⊥(ABC); (SBC)⊥(ABC);
Площадь ΔSAB = 9; площадь ΔSCD = 20
ΔSAB : SK⊥AB - высота, тогда площадь
S₁ = SK*AB/2 = 9; SK = 9*2/AB = 18/3 = 6; SK = 6
ΔSCD : SN⊥CD - высота, тогда площадь
S₂ = SN*CD/2 = 20; SN = 20*2/CD = 40/5 = 8; SN = 8
AB║CD по условию ⇒ ∠MAB = ∠MDC как соответственные углы ⇒
ΔAMB~ΔDMC по двум углам : ∠MAB = ∠MDC и общему углу М ⇒
Отношение высот треугольников пропорционально отношению сторон:
MK/MN = AB/CD = 3/5; ⇒ MK = 0,6 MN
---------------------------------------------------------
ΔSNM : h² = SM² = SN² - MN² = 8² - MN²
ΔSKM : h² = SM² = SK² - MK² = 6² - (0,6 MN)²
6² - (0,6 MN)² = 8² - MN²
MN² - 0,36 MN² = 64 - 36
0,64 MN² = 28
MN² = 43,75
NK = MN - NK = MN - 0,6 MN = 0,4 MN = 0,4*√43,75
NK = √7
h² = SN² - MN² = 64 - 43,75 = 20,25 = 4,5²
h = 4,5
----------------------------------------------------------
Объем пирамиды
V = S₀*h/3 = ((AB + CD)*NK/2) * h /3 = 4√7 * 4,5 / 3 = 6√7
V = 6√7