Вариант С номера 12, 13 и 14

Question

Дан 1 ответ

Правильный ответ

$12)\; \; \frac{a}{x+5}+\frac{b}{(x-2)^2}=\frac{x^2+24}{x^3+x^2-16x+20} \\\\\frac{a}{x+5}+\frac{b}{(x-2)^2}=\frac{a(x-2)^2+b(x+5)}{(x+5)(x-2)^2}=\frac{ax^2-4ax+4a+bx+5b}{(x+5)(x^2-4x+4)}=\\\\=\frac{ax^2+(-4a+b)x+4a+5b}{x^3-4x^2+4x+5x^2-20x+20}=\frac{a\cdot x^2+(b-4a)\cdot x+(4a+5b)}{x^3+x^2-16x+20}\; \; \Rightarrow \\\\ax^2+(b-4a)\cdot x+(4a+5b)=x^2+0\cdot x+24\\\\x^2\; |\; a=1\\x\; \; |\; b-4a=0\; \; ,\; \; b=4a=4\cdot 1=4\\x^0\; |\; 4a+5b=24\; \; ,\; \; 4\cdot 1+5\cdot 4=4+20=24\\\\Otvet:\; \; a=1\; ,\; b=4.$

$13)\; \; x^2+2xy=3x+6y+2\\\\x(x+2y)=3(x+2y)+2\\\\x(x+2y)-3(x+2y)=2\\\\(x+2y)(x-3)=2\; \; \Rightarrow \; \; \left \{ {{x+2y=2} \atop {x-3=1}} \right.\; ili\; \left \{ {{x+2y=1} \atop {x-3=2}} \right.\; ili\; \left \{ {{x+2y=-2} \atop {x-y=-1}} \right. \\\\ili\; \left \{ {{x+2y=-1} \atop {x-3=-2}} \right. \\\\a)\; \; \left \{ {{2y=2-x} \atop {x=1+3}} \right. \; \left \{ {{y=-1} \atop {x=4}} \right. \; \Rightarrow \; \; (4,-1)\\\\b)\; \; \left \{ {{2y=1-x} \atop {x=2+3}} \right.\; \left \{ {{2y=-4} \atop {x=5}} \right. \; \left \{ {{y=-2} \atop {x=5}} \right.\; \; \Rightarrow \; \; (5,-2)$

$c)\; \; \left \{ {{2y=-2-x} \atop {x=-1+3}} \right.\; \left \{ {{2y=-4} \atop {x=2}} \right.\; \left \{ {{y=-2} \atop {x=2}} \right. \; \; \Rightarrow \; \; (2,-2)\\\\d)\; \; \left \{ {{2y=-1-x} \atop {x=-2+3}} \right.\; \left \{ {{2y=-2} \atop {x=1}} \right. \; \left \{ {{y=-1} \atop {x=1}} \right. \; \; \Rightarrow \; \; (1,-1)\\\\Otvet:\; \; (4,-1)\; ,\; (5,-2)\; ,\; (2,-2)\; ,\; (1,-1)\; .$

$14)\; \; y=\frac{x-3}{|x|-1}\; \; ,\; \; ODZ:\; \; |x|-1\ne 0\; \; \Rightarrow \; \; x\ne \pm 1\\\\a)\; \; x\geq 0:\; \; y=\frac{x-3}{x-1}=1-\frac{2}{x-1}\; ;$

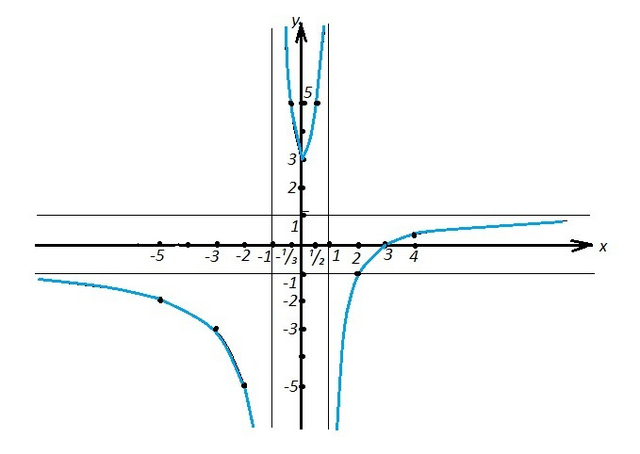
Это уравнение гиперболы, асимптоты которой имеют уравнения х=1 и у=1. Чтобы начертить этот график, надо начертить график гиперболы $y=-\frac{2}{x}$ . Ветви этой гиперболы будут расположены во 2 и 4 четвертях. Затем надо этот график сдвинуть относительно оси ОХ вправо на 1 единицу и относительно оси ОУ вверх тоже на 1 единицу. Так как х≥0, то останется та часть графика, которая находится в 1 и 4 четвертях.

$b)\; \; x<0:\; \; y=\frac{x-3}{-x-1}=\frac{x-3}{-(x+1)}=-\frac{(x+1)-1-3}{x+1}=\frac{4}{x+1}-1$

Это график гиперболы, асимптоты которой имеют уравнения х=-1 и у=4. Чтобы начертить график этой гиперболы, надо начертить график гиперболы $y=\frac{4}{x}$ , ветви которой будет расположены в 1 и 3 четвертях. Затем сдвинуть этот график относительно оси ОХ на 1 единицу влево и относительно оси ОУ на 1 единицу вниз.

NNNLLL54_zn (835k баллов) 11 Сен, 18