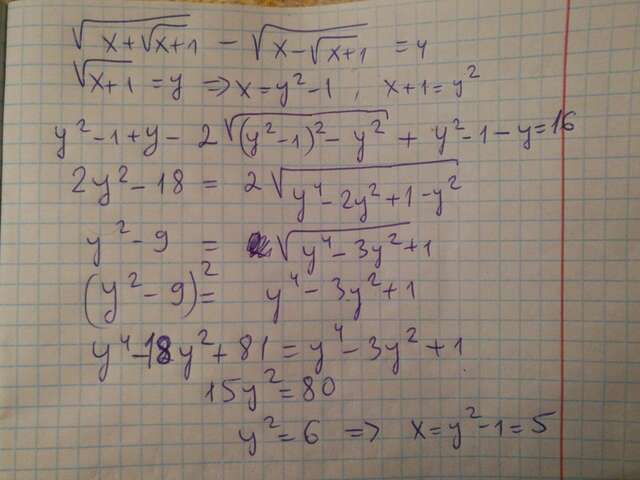![\sqrt[3]{x + 34} - \sqrt[3]{x - 3} = 1 \sqrt[3]{x + 34} - \sqrt[3]{x - 3} = 1](https://tex.z-dn.net/?f=+%5Csqrt%5B3%5D%7Bx+%2B+34%7D+-+%5Csqrt%5B3%5D%7Bx+-+3%7D+%3D+1)
делаем замену

x = {y}^{3} + 3" alt="y = \sqrt[3]{x - 3} \: = > x = {y}^{3} + 3" align="absmiddle" class="latex-formula">
тогда наше уравнение примет вид:
![\sqrt[3]{ {y}^{3} + 37 } - y = 1 \sqrt[3]{ {y}^{3} + 37 } - y = 1](https://tex.z-dn.net/?f=+%5Csqrt%5B3%5D%7B+%7By%7D%5E%7B3%7D+%2B+37+%7D+-+y+%3D+1)
![\sqrt[3]{ {y}^{3} + 37 } = y + 1 \sqrt[3]{ {y}^{3} + 37 } = y + 1](https://tex.z-dn.net/?f=+%5Csqrt%5B3%5D%7B+%7By%7D%5E%7B3%7D+%2B+37+%7D+%3D+y+%2B+1)
возводим в куб обе части
y³+37=y³+3y²+3y+1
3y²+3y-36=0
y²+y-12=0
(y+4)(y-3)=0
y1=-4
y2=3
Вернёмся к замене
x=y³+3
тогда
х1=(-4)³+3=-61
х2=3³+3=30
Ответ х1=-61, х2=30
второе уравнение на фото.
удачи!