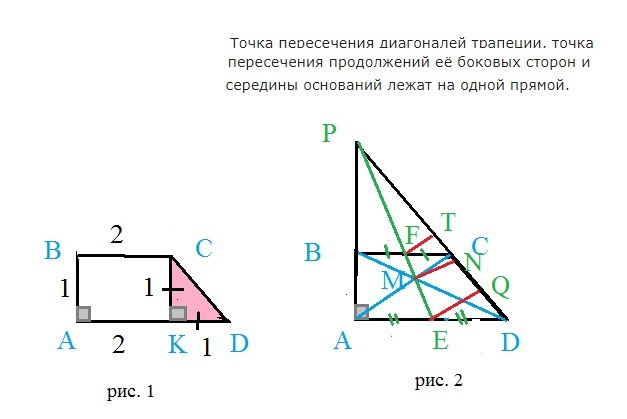
1) Рис. 1 легко увидеть, что ∠D=45°
2) Продолжаем стороны трапеции до пересечения в точке P.
см. рис.2
Применяем свойство трапеции ( см. там же)
Из подобия треугольников MFT и MED
FM:ME=ET:ED=1:1,5=2:3
Из прямоугольной трапеции ABFE
FE²=1²+(1,5-1)²=5/4
FE=(√5)/2
FM=(2/5)FE=(2/5)·((√5)/2)=(2√5)/10=0,2√5
MF=(3/5)FE=(3/5)·((√5)/2)=(3√5)/10=0,3√5
Проводим перпендикуляры из точек F,M,E на сторону СD
FT=FC·sin45°=1·(√2)/2=(√2)/2
EQ=ED·sin45°=1,5·(√2)/2=3·(√2)/4
Из подобия Δ PFC и PED
PF=√5
Из подобия Δ PFT и PMN
MN=PM·ET/PF=(1,2√5)·(√2/2)/(√5)=0,6√2
О т в е т. 0,6√2=(3√2)/5