А и В точки ** параболе у в квадрате=2рх, р больше 0.хорда АВ параллельна оси У. Через...

Question

А и В точки на параболе у в квадрате=2рх, р больше 0.хорда АВ параллельна оси У. Через точку А проведена касательная ,пересекающая прямую,парралельную оси Х и проходящую через В.1) Выразить через р геометрическое место точек С и начертить набросок . 2) Координата У точки С ,находящаяся на линии н7айденной в первой части, у=-2р. найти угол между касательной и осью Х в этом случае.

Answer 1

1.

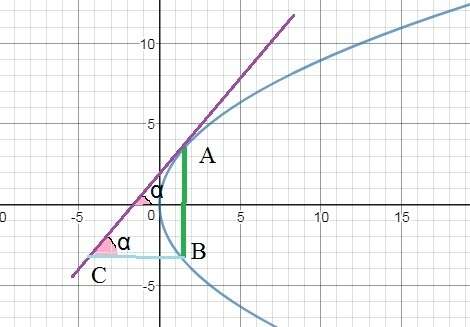
пусть A(x₀; √(2px₀)); B(x₀; - √(2px₀))

Ветвь параболы, на которой расположена точка А. задается уравнением y=√(2px);

y`=2p/(2√(2px))=√p/√(2x)

Уравнение касательной в точке А

y - √(2px₀) = (√p/√(2x₀)) ·( x - x₀)

Находим абсциссу точки С - точки пересечения касательной и прямой, проходящей через В

{ y - √(2px₀) = (√p/√(2x₀)) ·( x - x₀)

{y = - √(2px₀)

Получаем х=-3х₀

Значит С(-3х₀; - √(2px₀) )

2.

-2p= - √(2px₀)⇒ x₀ =2p

k_(касательной)=f ` (x₀ )=√p/√(2·2p)=1/2

tgα=1/2

α=arctg(1/2)

Из прямоугольного треугольника АВС

tgα=AB/BC=2·√(2px₀)/(4x₀)=[ при х₀=2p]=1/2

α=arctg(1/2)

---

Comments

извините,но надо найти не точку С , а геометрическое место точек ( все возможные точки) и начертить набросок полученной линии

---

Выразить координату y точки С через координату х: С(x;y) x=-3x₀, x₀=-x/3 Значит y=-√(2px₀) или у = - √(2p(-x/3))