Дано:
 м
м
 м
м
 м/с²
м/с²
===================
Найти: 

===================
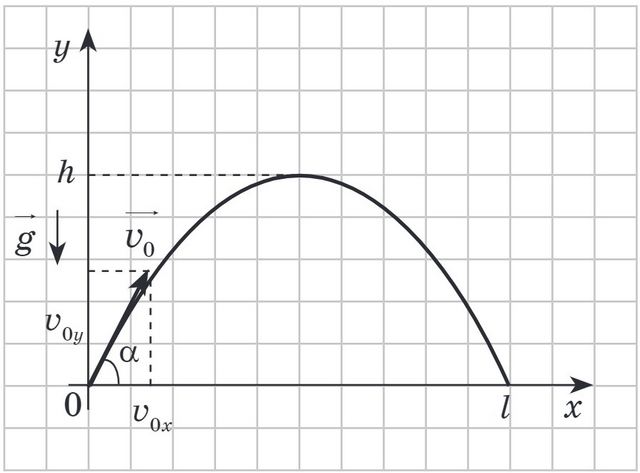
Решение. Движение тела, брошенного под углом к горизонту, является сложным: равномерным по ОХ и свободным падением по OY (см. рисунок).
Максимальную высоту при этом можно определить по формуле (1):
 ,
,
а дальность полёта - по формуле (2):

Разделим уравнение (1) на уравнение (2), получим:
 , откуда
, откуда  .
.
Выполним расчёты:  , тогда
, тогда  .
.
Из уравнения (1) найдём:  .
.
Проверим единицы и определим числовое значение бросания тела:
![[v_{0}] = \sqrt{\frac{_{M} \cdotp _{M}}{c^{2}}} = \sqrt{\frac{_{M^{2}}}{c^{2}}} = \frac{_{M}}{c} [v_{0}] = \sqrt{\frac{_{M} \cdotp _{M}}{c^{2}}} = \sqrt{\frac{_{M^{2}}}{c^{2}}} = \frac{_{M}}{c}](https://tex.z-dn.net/?f=+%5Bv_%7B0%7D%5D+%3D+%5Csqrt%7B%5Cfrac%7B_%7BM%7D+%5Ccdotp+_%7BM%7D%7D%7Bc%5E%7B2%7D%7D%7D++++%3D++%5Csqrt%7B%5Cfrac%7B_%7BM%5E%7B2%7D%7D%7D%7Bc%5E%7B2%7D%7D%7D+%3D+%5Cfrac%7B_%7BM%7D%7D%7Bc%7D++) ;
;

Ответ: тело бросили с начальной скоростью υ₀ ≈ 22,2 м/с под углом α = 27° к горизонту.