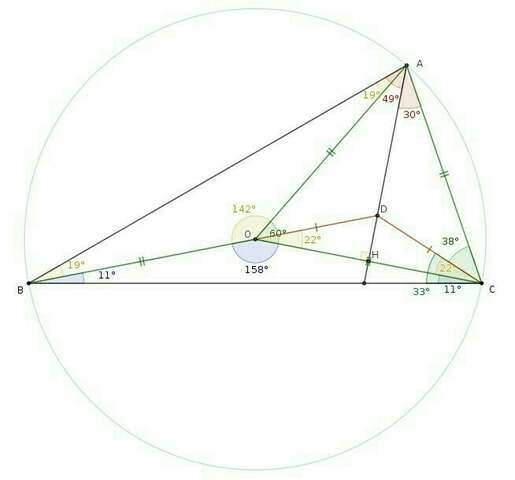
Сделаем следующим образом:
1) Пусть точка О - это центр описанной окружности около ∆ АВС, тогда
угол АОС является центральным углом, угол АВС — вписанным углом => по свойству вписанного угла:
угол АОС = 2 × угол АВС = 2 × 30° = 60°
Аналогично, угол АОВ = 2 × угол АСВ = 2 × 71° = 142°
угол ВОС = 2 × угол ВАС = 2 × 79° = 158°
Следовательно, ∆ АОВ, ∆ ВОС - равнобедренные, ∆ АОС - равносторонний ( угол при вершине равен 60° ). Тогда...
2) Рассмотрим ∆ АОВ ( АО = ОВ ) :
угол ОВА = угол ОАВ = ( 180° - 142° ) : 2 = 38° : 2 = 19°
Рассмотрим ∆ ВОС ( ОВ = ОС ) :
угол ОВС = угол ОСВ = ( 180° - 158° ) : 2 = 22° : 2 = 11°
Из этого следует, что точка О, центр описанной окружности, лежит на отрезке BD ( O € BD )
3) угол DOC = 180° - угол BOC = 180° - 158° = 22°
угол CDO = угол DCB - угол ОСВ = 33° - 11° = 22°
Значит, ∆ ОDС - равнобедренный. Соответственно, ∆ АОD = ∆ ACD по двум сторонам и углу между ними =>
точка D лежит на высоте АН треугольника АОС ( D € АН )
угол OAD = угол CAD = 1/2 × угол ОАС = 1/2 × 60° = 30°
Значит, угол ВАD = a = угол ВАС - угол САD = 79° - 30° = 49°
ОТВЕТ: 49°