7/(x ² - 9)≥ 1
7/(x² - 9)- 1≥ 0
(7 - x² + 9)/ (x²- 9)≥0
(16 - x²)/(x² - 9) ≥0
построим графики
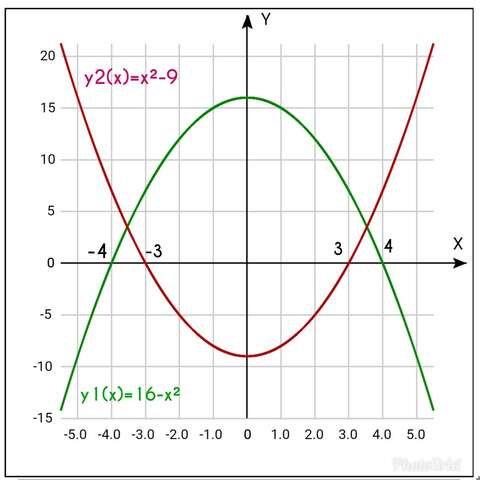
y1(x)=16-x² и y2(x)=x²-9 (см фото)
их легко построить, если взять за основу параболу х².
Наше неравенство будет соблюдено , если y1 (x)и у2(x) будут одного знака,
откуда получаем решение ( с учётом области определения x²-9≠0 или х≠±3)
x€[-4, -3)v(-3, 4]
Получаем, что целочисленные решения будут
-4, +4
Их два
Ответ (1) два решения
удачи Вам!