№1
Находим отношения всех соответствующих коэфициентов уравнений данной системы: -0,9 : 9 = -0,1; 5 : (-50) = -0,1; 4 : 40 = 0,1.
Поскольку первые два отношения равны, а третье- нет, то система не имеет решений. Ответ: нет решений.
№2
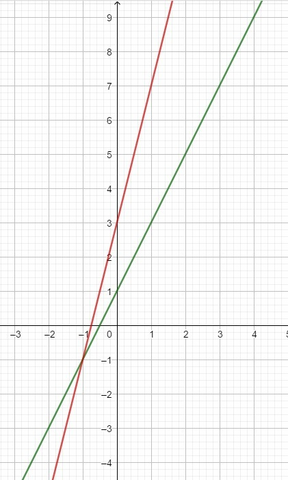
Чтобы система имела единственное решение надо, чтобы отношение коэфициентов при соответствующих переменных были не равны. Например такая система: у - 2х = 1 и у - 4х = 3. Чтобы решить эту систему графически, выражаем у через х в каждом уравнении: у = 2х + 1 и у = 4х + 3. После этого строим прямые, которые являются графиками каждого уравнения. Решением системы будет пара чисел, которая является координатами точки пересечения прямых. (Рисунок во вложении)
№3.
Воспользуемся уравнением прямой, проходящей через две точки:
(х - х₁)/(х₂ - х₁) = (у - у₁)/(у₂ - у₁), где (х₁; у₁) и (х₂; у₂) - координаты даных точек (в нашем случае А и В)
Имеем: (х + 3)/(0 + 3) = (у - 0)/(9 - 0); (х + 3)/3 = у/9| · 9; 3(х + 3) = у; y = 3x + 9.
Ответ: y = 3x + 9