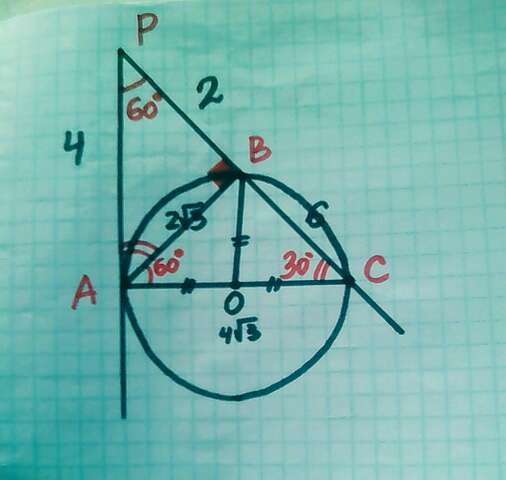
1) угол PAB = угол АСВ = 30° - по теореме угла между касательной и хордой
угол АРВ + угол РАВ = 60° + 30° = 90°
Значит, ∆ АРВ и ∆ АВС прямоугольные =>
АС - диаметр окружности, так как прямой угол в окружности всегда опирается на диаметр окружности
2) Рассмотрим ∆ РАС :
Катет, лежащий против угла в 30°, равен половине гипотенузы =>
РС = 2 × АР = 2 × 4 = 8
ВС = РС - РВ = 8 - 2 = 6
3) Рассмотрим ∆ РАВ:
По теореме Пифагора:
АВ² = 4² - 2² = 16 - 4 = 12
АВ = 2√3
4) Рассмотрим ∆ АВС:
Катет, лежащий против угла в 30°, равен половине гипотенузы =>
АС = 4√3
АО = ОС = 2√3 - радиусы окружности
5) Площадь сектора АОВ равна:
S = πR² × a / 360° = π × ( 2√3 )² × 60° / 360° = 2π
a = угол АОВ
6) Площадь ∆ ВОС:
S = abc / 4R = ( 2√3 × 2√3 × 6 ) ÷ ( 4 × 2√3 ) = 3√3
В итоге площадь заштрихованной области равна:
S = 2π + 3√3
ОТВЕТ: 2π + 3√3