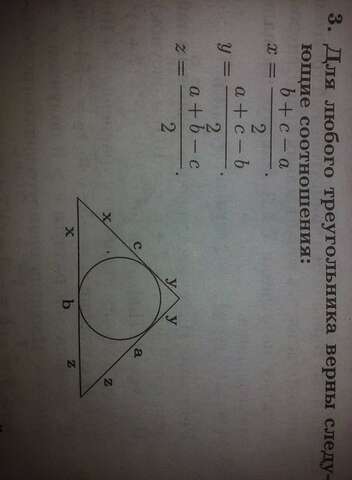
Пусть у нашего равнобедренного треугольника боковая сторона будет a, основание будет b и его боковые стороны равны
Так как окружность делит боковую сторону в отношении 3:2 начиная от основания, то её можно представить в виде a=3x+2x. По свойству вписанной в треугольник окружности (см. картинку внизу) можно выразить все через первую формулу, как:
6x = b+3x+2x-3x-2x ⇒ b = 6x.
Зная, что периметр равнобедренного треугольника равен 48, можно записать это как: Р = 48 = 2a+b = 10x+b, и подставить в систему уравнения, чтобы найти основание b:
\left \{ {{b=6x} \atop {10x+6x=48}} \right. => \left \{ {{b=6x} \atop {16x=48}} \right. => \left \{ {{b=18} \atop {x=3} \right. " alt=" \left \{ {{b=6x} \atop {2a+b=48}} \right. => \left \{ {{b=6x} \atop {10x+6x=48}} \right. => \left \{ {{b=6x} \atop {16x=48}} \right. => \left \{ {{b=18} \atop {x=3} \right. " align="absmiddle" class="latex-formula">
Зная периметр и основание равнобедренного треугольника, можно найти его боковую сторону:
P = 2a+b ⇒ 2a = P-b = 48-18 = 30 ⇒ a=15. Проверяем наш ответ: 15+15+18 = 48, что удовлетворяет условию задачи.
Ответ: боковая сторона равна 15 см.
