Помогите пожалуйста Надо решить или методом ОХа, или графическим, или аналитическим. Фото...

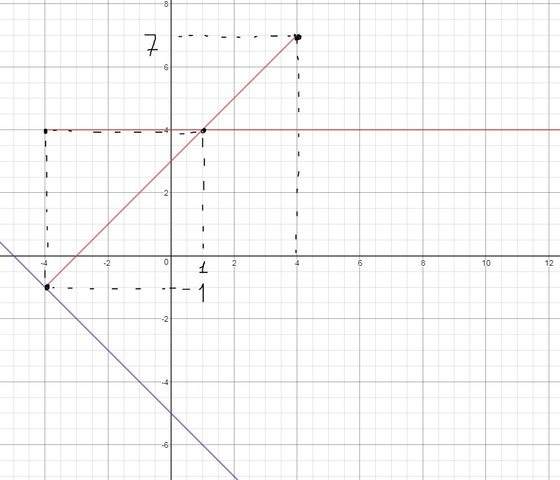
Можно и аналитически, но так нагляднее.

ограничения:

$\left \{ {{y<7} \atop {x\geq-4}} \right.$

И, собственно решения:

$y=4; y=x+3$

нижнее уравнение:

$y=a-x$

Как будем вычислять параметр a? Просто складывать координату точки пересечения (x+y)

1) $a=-4-1=-5$

2) $a=-4+4=0$

3) $a=4+1=5$

4) $a=7+4=11$

Собственно далее выбираете нужные вам промежутки a под кол-во решений

P.S. Как решить аналитически? Выразить из нижнего уравнения x и подставить в верхнее. Кстати, что за метод Оха? 1 раз слышу