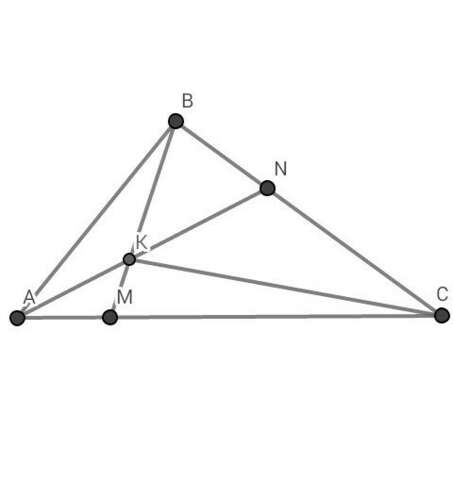
ДАНО: ∆ АВС ; АМ : МС = 1 : 5 ; ВN : NC = 1 : 2
НАЙТИ: ВК : КМ
____________________________
РЕШЕНИЕ:
Если у двух треугольников есть общая высота, то их площади относятся как основания
S bkn / S nkc = 1 /2
S akm / S mkc = 1 / 5
Если угол одного треугольника равен углу другого треугольника, то их площади относятся как произведения сторон, заключающих равные углы.
S bmc / S anc = 3 × 5 / 2 × 6 = 5 / 4
Пусть S bkn = x , S akm = y , тогда
S nkc = 2x , S kmc = 5y
S bmc = S bkn + S nkc + S kmc = x + 2x + 5y = 3x + 5y
S anc = S akm + S kmc + S nkc = y + 5y + 2x = 6y + 2x

Если у двух треугольников есть общая высота, то их площади относятся как основания
S bkc / S kmc = ( x + 2x ) / 5y = ( 5y + 10y ) / 5y = 15y / 5y = 3 : 1
Значит, ВК : КМ = 3 : 1
ОТВЕТ: 3