Помогите решить . Много баллов.!!!!

Найдём область допустимых значений функции (ОДЗ) и упростим функцию.

$y=\frac{(0,5x^2+2x)\cdot |x|}{x+4}\; ,\; \; \; ODZ:\; \; x+4\ne 0\; ,\; x\ne -4\\\\\frac{(0,5x^2+2x)\cdot |x|}{x+4}=\frac{(\frac{1}{2}\cdot x^2+2x)\cdot |x|}{x+4}=\frac{(x^2+4x)\cdot |x|}{2\cdot (x+4)}=\frac{x\cdot (x+4)\cdot |x|}{2\cdot (x+4)}=\frac{x\cdot |x|}{2}\; \Rightarrow \\\\y=\frac{1}{2}\cdot |x|\cdot x\; ,\; x\ne -4\\\\1)\; \; x\geq 0\; \; \to \; \; |x|=x\; \; \to \; \; y=\frac{1}{2}\cdot x^2\\\\2)\; \; x<0\; \to \; \; |x|=-x\; \; \to \; \; y=-\frac{1}{2}\cdot x^2$

$y=\frac{1}{2}\cdot |x|\cdot x=\left \{ {{\frac{1}{2}\cdot x^2\; ,\; esli\; x\geq 0\; ,} \atop {-\frac{1}{2}\cdot x^2\; ,\; esli\; x\in (-\infty ,-4)\cup (-4,0)\; .}}$

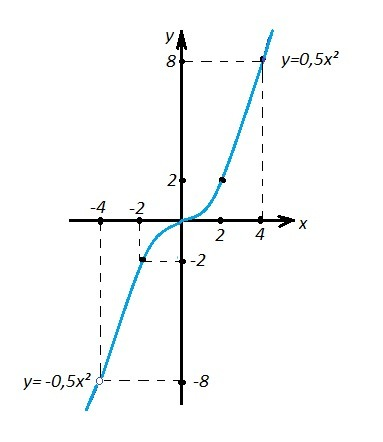
Прямая у=m - это прямая, параллельная оси ОХ. Единственная прямая, не имеющая общих точек с графиком заданной функции, параллельная оси ОХ, - это прямая у= -8 (в точке (-4,-8) заданная функция не определена, х≠ -4).