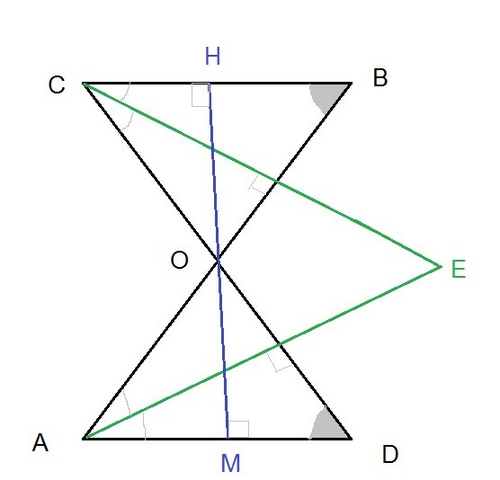
AB=CD
AO=OB и СО=OD ⇒ AO=OB=CO=OD
AO=AD ⇒ AO=OD=AD ⇒
а)Δ AOD - равносторонний. Все его углы 60 °
Δ BOC - равнобедренный, ∠BOC=∠AOD = 60 ° как вертикальные.
Значит ∠OBC=OCB=60 градусов.
Δ BOC - равносторонний.
б) ВС || AD так как внутренние накрест лежащие углы равны:
∠СВО=∠DAO
в)ОМ - медиана, а значит и высота и биссектриса равностороннего треугольника ADO.
OM < OA=CO
OM < CO
г)∠ АЕС=60 градусов. Биссектриса СЕ - высота и медиана равностороннего треугольника ВОС
Биссектриса АЕ - высота и медиана равностороннего треугольника АОD
∠BOD=120 ° как смежный с ∠ AOD
Сумма углов четырёхугольника OKEF равна 360 °
∠ОКЕ=∠OFE=90 °
д) Да.
OM ⊥ AD
OН ⊥ BC ( ОН - медиана, а значит и высота)
Из точки О можно провести один перпендикуляр к параллельным прямым АD и ВС.
Треугольники ВОС и AOD равны. Значит и высоты OM и OH тоже равны. O- середина MH.