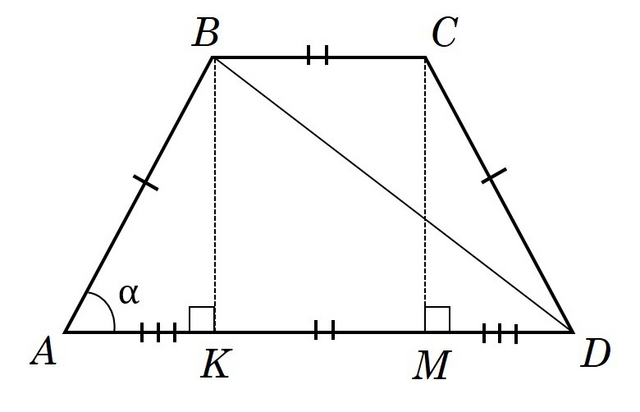
Дано: чотирикутник ABCD - рівнобічна трапеція (AB = CD); ∠BAD = 60°, BD = 14 см.
Знайти: BC - ?
Розв'язання. Нехай х см - довжина більшої основи (AD) трапеції. Тоді (х - 10)см - довжина бокової сторони трапеції (AB). Скористаємося теоремою косінусів - твердженням про властивість довільних трикутників, що є узагальненням теореми Піфагора.
BD² = AD² + AB² - 2 × AD × AB × cos∠BAD
14² = x² + (x - 10)² - 2 × x × (x - 10) × cos60°
196 = x² + x² - 20x + 100 - 2(x² - 10x) × 1/2
196 = x² - 10x + 100
x² - 10x - 96 = 0
Скористаємося теоремою Вієта:
х₁ + х₂ = 10
х₁ × х₂ = -96
x₁ = -6 (не задовольняє умові задачі); x₂ = 16
Тоді АD = 16 см, а AB = 16 - 10 = 6 см.
Для того, щоб знайти меншу основу рівнобічної трапеції проведемо дві висоти ВК та СМ з точок В і С відповідно (див. рисунок). Вони утворюють прямокутник, у якого менша основа трапеції ВС дорівнює відрізку КМ, який належить більшій основі AD.
KM = AD - AK - MD = AD - 2AK (тому що AK = MD).
Щоб знайти відрізок АК, розглянемо трикутник АВК (∠AKB = 90°):
cosα = AK/AB ⇒ AK = AB × cosα = 6 × 1/2 = 3 (cм)
Отже, KM = AD - 2AK = 16 - 2 × 3 = 10 (см) = BC
Відповідь: ВС = 10 см.