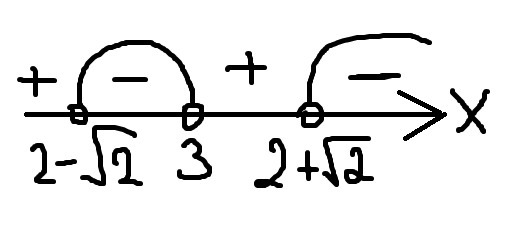1 \\ \\ ODZ: 3-x\ne 0 \ ; \ x \ne 3 \\ \\ \dfrac{x(3-x)+1-3+x}{3-x} > 0 \\ \\ \dfrac{3x-x^{2} - 2 + x}{3-x} > 0 \ \ / *(-1) \\ \\ \dfrac{x^{2} - 4x + 2}{3-x}< 0 \\ \\ \dfrac{(x-2+\sqrt{2})(x-2-\sqrt{2})}{3-x}< 0 \ (1) \\ \\ x \in (2-\sqrt{2};3)\cup (2+\sqrt{2} ; +\infty) " alt=" x + \dfrac{1}{3-x}> 1 \\ \\ ODZ: 3-x\ne 0 \ ; \ x \ne 3 \\ \\ \dfrac{x(3-x)+1-3+x}{3-x} > 0 \\ \\ \dfrac{3x-x^{2} - 2 + x}{3-x} > 0 \ \ / *(-1) \\ \\ \dfrac{x^{2} - 4x + 2}{3-x}< 0 \\ \\ \dfrac{(x-2+\sqrt{2})(x-2-\sqrt{2})}{3-x}< 0 \ (1) \\ \\ x \in (2-\sqrt{2};3)\cup (2+\sqrt{2} ; +\infty) " align="absmiddle" class="latex-formula">
Ответ: x ∈ (2-√2; 3)∪(2+√2; + ∞)
