В прямоугольном треугольнике ABC с прямым углом C, угол B=60∘ . Найдите соотношение...

Question

В прямоугольном треугольнике ABC с прямым углом C, угол B=60∘ . Найдите соотношение AH:HC, где H — точка пересечения серединного перпендикуляра к гипотенузе с катетом AC

Comments

учитывая что б 60 градусов а он прямоугольный то ц 90градусов, а угол а следовательно 30, помнится существует теорема про 30 градусов

Answer 1

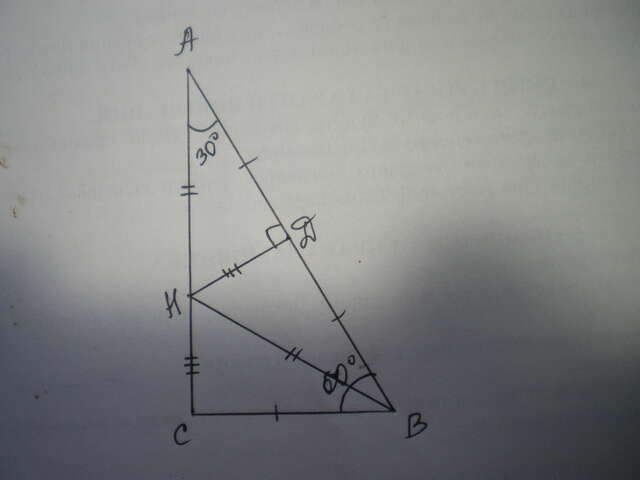
Дано: ΔАВС - прямоугольный, ∠С=90°, ∠В=60° ДН⊥АВ, АД=ВД.

Найти АН:СН.

Проведем ВН. Рассмотрим ΔАВН - равнобедренный, т.к. АД=ВД, ДН - высота и медиана. Значит, ВН=АН.

В ΔАВС ∠А=90-60=30°. Значит, ВС=1\2АВ=АД=ВД

ΔАДН=ΔВДН по трем сторонам, значит ∠ДВН=∠А=30°

Рассмотрим ΔАДН - прямоугольный.

ДН лежит против ∠30°, значит ДН=1\2АН.

ΔВДН=ΔСВН по двум сторонам и углу между ними

значит ДН=СН

но ДН=1\2АН, значит и СН=1\2АН,

отсюда следует, что АН:СН=2:1.

Ответ: 2:1.

---