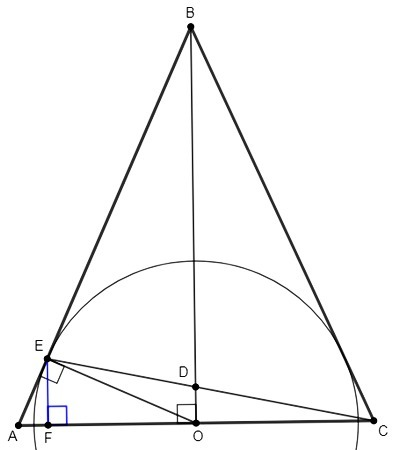
AB=BC, E - точка касания на AB, CD:DE=6:5, O - центр окружности
Окружость вписана в угол B, следовательно её центр лежит на биссектрисе этого угла. В равнобедренном треугольнике биссектриса к основанию является высотой и медианой, BO⊥AC, AO=CO.
Опустим перпендикуляр EF на AC.
EF || DO => CO:OF=6:5 (по теореме Фалеса)
AO:OF=6:5
AO=6x, OF=5x => AF=x
Высота из прямого угла равна среднему пропорциональному проекций катетов на гипотенузу.
EF=√(AF*OF) =x√5
Высота из прямого угла делит треугольник на подобные друг другу и исходному.
△EOF~△AOE, △AOE~△ABO => △ABO~△EOF, k=AO/EF =6/√5 =1,2√5
AB=EO*k =1,2√5 EO
S(ABC)= 2S(ABO) =AB*EO =1,2√5 EO^2 =10,8√5 ~24,15