Отрезок включает крайние точки.
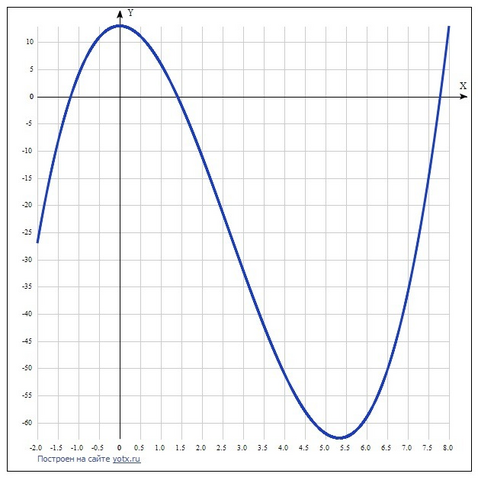
Даны функция у = x³ - 8х² + 13 и отрезок [-5; 5]
Находим производную: y' = 3x² - 16x и приравниваем её нулю.
3x² - 16x = 0.
х(3x - 16) = 0.
Отсюда находим 2 критические точки: х = 0 и х = 16/3.
Исследуем их на экстремум.
На промежутках находим знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x =-1045,3333 6
y' =190-16 0 12
.
Значит, максимум в точке х= 0, которая входит в заданный промежуток.
В точке х = 16/3 = 5,3333 имеем минимум, поэтому не заданном промежутке нет значения больше, чем в точке х = 0.
Ответ: у(макс) = 13.