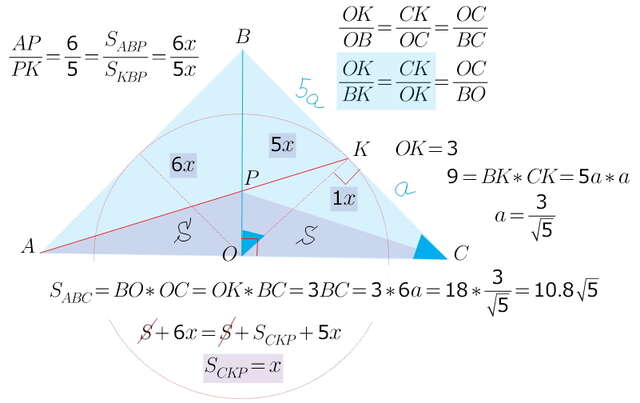
известно: площади треугольников с равными высотами относятся как основания (это речь про данное отношение 6:5)
рассмотрев еще один равнобедренный треугольник (АРС), найдем отношение ВК:КС = 5:1
радиус ОК ⊥ ВС (касательной к окружности) и является высотой к гипотенузе прямоугольного треугольника ОВС
известно: высота к гипотенузе=среднему геометрическому отрезков гипотенузы ОК*ОК = ВК*СК (то же самое получится, если рассмотреть подобные прямоугольные треугольники)