Чтобы квадратное уравнение имело 2 различных корня необходимо, чтобы дискриминант был строго больше нуля.
Напомню:
D < 0 - уравнение не имеет корней,
D = 0 - уравнение имеет два одинаковых корня,
D > 0 - уравнение имеет два различных корня.
Формула вычисления дискриминанта в общем виде для уравнения такого вида 

Приступим к решению.
1) Найдём дискриминант:

2) Подставим в неравенство D > 0:
 0, " alt=" a^2 - 64 > 0, " align="absmiddle" class="latex-formula">
0, " alt=" a^2 - 64 > 0, " align="absmiddle" class="latex-formula">
 64. " alt=" a^2 > 64. " align="absmiddle" class="latex-formula">
64. " alt=" a^2 > 64. " align="absmiddle" class="latex-formula">
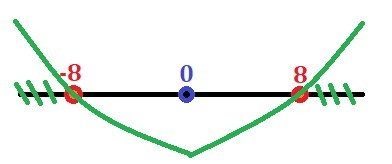
Так как коэффициент при x² больше нуля, ветви параболы направлены вверх. Исходя из этого строим рисунок, получаем совокупность неравенств, которая и является ответом.
 8.\\\end{array} " alt=" \left[\begin{array}{ccc}a < -8,\\a > 8.\\\end{array} " align="absmiddle" class="latex-formula">
8.\\\end{array} " alt=" \left[\begin{array}{ccc}a < -8,\\a > 8.\\\end{array} " align="absmiddle" class="latex-formula">
3) Таким образом, получаем:
a ∈ (-∞; -8) U (8; +∞).
Ответ: 5) (-∞; -8) U (8; +∞).