Решить неравенство :
 log_{1+2cosx}(2+cosx) " alt=" log_{1+2cosx}(1 + 3sinx)>log_{1+2cosx}(2+cosx) " align="absmiddle" class="latex-formula">
log_{1+2cosx}(2+cosx) " alt=" log_{1+2cosx}(1 + 3sinx)>log_{1+2cosx}(2+cosx) " align="absmiddle" class="latex-formula">
ОДЗ основания логарифма
 0} \atop {1+2cosx\neq}1} \right.;\left \{ {{2cosx>-1} \atop {2cosx\neq}0} \right. ;\left \{ {{cosx>-0,5} \atop {cosx\neq}0} \right.\\ \\ \left \{ {{-2\pi/3+2\pi k0} \atop {1+2cosx\neq}1} \right.;\left \{ {{2cosx>-1} \atop {2cosx\neq}0} \right. ;\left \{ {{cosx>-0,5} \atop {cosx\neq}0} \right.\\ \\ \left \{ {{-2\pi/3+2\pi k
0} \atop {1+2cosx\neq}1} \right.;\left \{ {{2cosx>-1} \atop {2cosx\neq}0} \right. ;\left \{ {{cosx>-0,5} \atop {cosx\neq}0} \right.\\ \\ \left \{ {{-2\pi/3+2\pi k0} \atop {1+2cosx\neq}1} \right.;\left \{ {{2cosx>-1} \atop {2cosx\neq}0} \right. ;\left \{ {{cosx>-0,5} \atop {cosx\neq}0} \right.\\ \\ \left \{ {{-2\pi/3+2\pi k
ОДЗ подлогарифмических выражений
 0} \atop {2+cosx>0}} \right. ;\left \{ {{3sinx>-1} \atop {cosx>-2}} ;\left \{ {{sinx>-1/3} \atop {x:R}} \right. \right.; \\ \\ \left \{ {{-arcsin(1/3)+2\pi k0} \atop {2+cosx>0}} \right. ;\left \{ {{3sinx>-1} \atop {cosx>-2}} ;\left \{ {{sinx>-1/3} \atop {x:R}} \right. \right.; \\ \\ \left \{ {{-arcsin(1/3)+2\pi k
0} \atop {2+cosx>0}} \right. ;\left \{ {{3sinx>-1} \atop {cosx>-2}} ;\left \{ {{sinx>-1/3} \atop {x:R}} \right. \right.; \\ \\ \left \{ {{-arcsin(1/3)+2\pi k0} \atop {2+cosx>0}} \right. ;\left \{ {{3sinx>-1} \atop {cosx>-2}} ;\left \{ {{sinx>-1/3} \atop {x:R}} \right. \right.; \\ \\ \left \{ {{-arcsin(1/3)+2\pi k
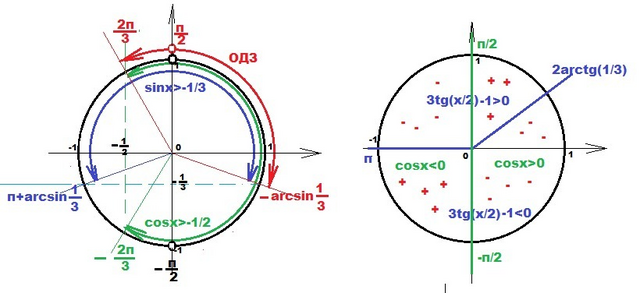
ОДЗ: x ∈ (-arcsin(1/3)+2πk; π/2+2πk)∪(π/2+2πk; 2π/3+2πk); k∈Z
 log_{1+2cosx}(2+cosx) " alt=" log_{1+2cosx}(1 + 3sinx)>log_{1+2cosx}(2+cosx) " align="absmiddle" class="latex-formula">
log_{1+2cosx}(2+cosx) " alt=" log_{1+2cosx}(1 + 3sinx)>log_{1+2cosx}(2+cosx) " align="absmiddle" class="latex-formula">
Так как основания логарифмов содержат переменную х, то решение неравенства разбивается на 2 случая: основание больше единицы и основание положительное меньше единицы.
1)
 1} \atop {1+3sinx>2+cosx}} \right. ;\left \{ {{cosx>0} \atop {3sinx-cosx-1>0}} \right.\\ \\ a)cosx>0;-\frac{\pi}{2}+2\pi k1} \atop {1+3sinx>2+cosx}} \right. ;\left \{ {{cosx>0} \atop {3sinx-cosx-1>0}} \right.\\ \\ a)cosx>0;-\frac{\pi}{2}+2\pi k
1} \atop {1+3sinx>2+cosx}} \right. ;\left \{ {{cosx>0} \atop {3sinx-cosx-1>0}} \right.\\ \\ a)cosx>0;-\frac{\pi}{2}+2\pi k1} \atop {1+3sinx>2+cosx}} \right. ;\left \{ {{cosx>0} \atop {3sinx-cosx-1>0}} \right.\\ \\ a)cosx>0;-\frac{\pi}{2}+2\pi k
Для второго неравенства системы можно воспользоваться формулами универсальной тригонометрической подстановки, так как по ОДЗ
x ≠ π + 2πk
b) 3sinx - cosx - 1 > 0
 0\\ \\ \dfrac{6tg\frac{x}{2}-1+tg^2\frac{x}{2}-1-tg^2\frac{x}{2}}{1+tg^2\frac{x}{2}} >0\\ \\ \dfrac{6tg\frac{x}{2}-2}{1+tg^2\frac{x}{2}} >0 " alt="3*\dfrac{2tg\frac{x}{2}}{1+tg^2\frac{x}{2}} -\dfrac{1-tg^2\frac{x}{2}}{1+tg^2\frac{x}{2}} -1>0\\ \\ \dfrac{6tg\frac{x}{2}-1+tg^2\frac{x}{2}-1-tg^2\frac{x}{2}}{1+tg^2\frac{x}{2}} >0\\ \\ \dfrac{6tg\frac{x}{2}-2}{1+tg^2\frac{x}{2}} >0 " align="absmiddle" class="latex-formula">
0\\ \\ \dfrac{6tg\frac{x}{2}-1+tg^2\frac{x}{2}-1-tg^2\frac{x}{2}}{1+tg^2\frac{x}{2}} >0\\ \\ \dfrac{6tg\frac{x}{2}-2}{1+tg^2\frac{x}{2}} >0 " alt="3*\dfrac{2tg\frac{x}{2}}{1+tg^2\frac{x}{2}} -\dfrac{1-tg^2\frac{x}{2}}{1+tg^2\frac{x}{2}} -1>0\\ \\ \dfrac{6tg\frac{x}{2}-1+tg^2\frac{x}{2}-1-tg^2\frac{x}{2}}{1+tg^2\frac{x}{2}} >0\\ \\ \dfrac{6tg\frac{x}{2}-2}{1+tg^2\frac{x}{2}} >0 " align="absmiddle" class="latex-formula">
Так как знаменатель дроби 1+tg²(x/2)≥1, то знак неравенства зависит только от числителя
6 tg (x/2) - 2 > 0
tg (x/2) > 1/3
arctg (1/3) + πm < x/2 < π/2 + πm, m ∈ Z
2arctg (1/3) + 2πm < x < π + 2πm
С учетом первого неравенства и ОДЗ
x ∈ (2arctg (1/3) + 2πk; π/2 + 2πk), k ∈ Z
2)

a) -0,5 < cosx < 0. Решение состоит из двух интервалов
x ∈ (-2π/3 + 2πk; -π/2+2πk) - не подходит под ОДЗ
x ∈ (π/2 + 2πk; 2π/3 + 2πk)
b) Второе неравенство решается аналогично первой системе с помощью универсальной тригонометрической подстановки, только со знаком '<'</p>
6 tg (x/2) - 2 < 0
tg (x/2) < 1/3
-π/2 + πp < x/2 < arctg (1/3) + πp, p∈Z
-π + 2πp < x < 2 arctg (1/3) + 2πp
Так как из первого неравенства x ∈ (π/2 + 2πk; 2π/3 + 2πk)
, то данная система не имеет решений.
Ответ: x ∈ (2 arctg(1/3) + 2πk; π/2+2πk); k∈Z
==========================================
2 способ. Покороче.
ОДЗ: x ∈ (-arcsin(1/3)+2πk; π/2+2πk)∪(π/2+2πk; 2π/3+2πk); k∈Z
Метод рационализации.Неравенство
 log_{1+2cosx}(2+cosx) " alt=" log_{1+2cosx}(1 + 3sinx)>log_{1+2cosx}(2+cosx) " align="absmiddle" class="latex-formula">
log_{1+2cosx}(2+cosx) " alt=" log_{1+2cosx}(1 + 3sinx)>log_{1+2cosx}(2+cosx) " align="absmiddle" class="latex-formula">
при всех допустимых значениях х равносильно неравенству

Для sinx и cosx в скобках использованы формулы универсальной тригонометрической подстановки через tg(x/2). Такая замена возможна, так как x = π + 2πh, h∈Z, в ОДЗ не входят. (п.1)

Знаки неравенства для интервала (-π; +π) с периодом 2πk
...... (-π) ++++++ (-π/2) ------- (2arctg(1/3)) ++++++ (π/2) ------ (π).......>x
С учетом периода и ОДЗ: x ∈ (2 arctg(1/3) + 2πk; π/2+2πk); k∈Z