В треугольнике АБС с углом ВАС, равным 24 градусам, ** сторонах АВ и АС взяты точки X и Y...

Question

В треугольнике АБС с углом ВАС, равным 24 градусам, на сторонах АВ и АС взяты точки X и Y соответственно. При этом окружность с центром в Y, проходящая через А, проходит также через X, а окружность с центром в X, проходящая через В, проходит также через С и Y. Найдите ∠АВС.

Answer 1

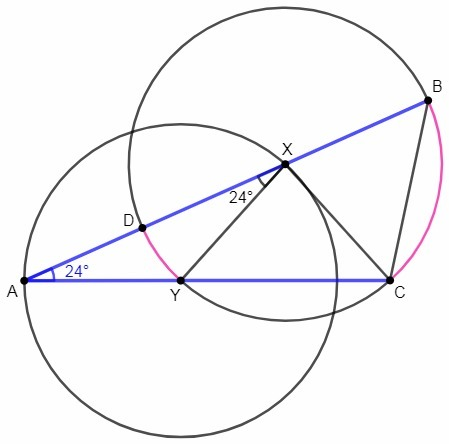
YA=YX (радиусы), △AYX - равнобедренный, ∠AXY=∠A

Центральный угол равен дуге, на которую опирается.

∪DY=∠DXY=∠A

Угол между секущими равен полуразности высекаемых дуг.

∠A= (∪BC-∪DY)/2 <=> ∪BC=2∠A+∪DY =3∠A

∠BXC=∪BC=3∠A

XB=XC (радиусы), △BXC - равнобедренный, ∠B=∠BCX

∠B=(180°-∠BXC)/2 = 90° -3/2 ∠A =54°

---