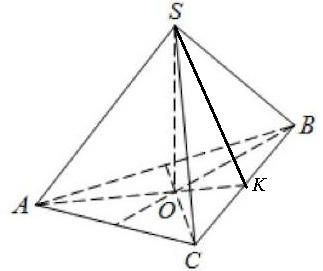
Из условия SA=SB=SC=13 см; ABC - правильный треугольник; AC=BC=AB=10 см. Найдем высоту одной из граней. Например, рассмотрим треугольник SBC: SK - высота грани; CK = BK = BC/2 = 5 см
Из прямоугольного треугольника SKB:  см
см
 см²
см²
Площадь боковой поверхности равна сумма площадей всех граней.
 см²
см²
Ответ: 180 см².