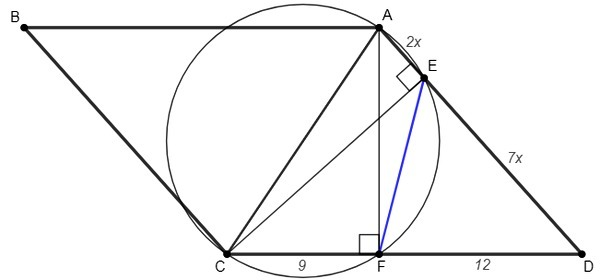
Диагональ AC параллелограмма ABCD служит диаметром окружности,которая пересекает стороны...

Question

Диагональ AC параллелограмма ABCD служит диаметром окружности,которая пересекает стороны AD и CD в точках E и F соответственно.Найти площадь параллелограмма, если известно,что AE:ED=2:7,CF=9см, DF=12см

Answer 1

Диагональ делит параллелограмм пополам. Рассмотрим треугольник ACD.

∠AFC, ∠AEC - вписанные углы, опирающиеся на диаметр - прямые. E, F - основания высот треугольника ACD. Отрезок, соединяющий основания высот треугольника, отсекает подобный треугольник, △FED~△ACD.

ED/CD = FD/AD <=> 7x/21 = 12/9x <=> x=2

AD=9x=18

AF=√(AD^2 -FD^2) =√(18^2 -12^2) =√(6*30) =6√5

S(ACD)= CD*AF/2 =21*6√5/2 =63√5

S(ABCD)= 2S(ACD) =126√5

---

Comments

CD*AF - ответ. Делить на 2, а потом умножать на 2 - не обязательно :)