записав ОДЗ: 2ˣ ≠ 5/3 и 4ˣ ≠ 1/(х+1),
т.е. х ≠ log₂(5/3) и х ≠ 0...
по свойству пропорции получим уравнение:
5х - 3х * 2ˣ = 8х * 4ˣ +8 * 4ˣ - 8
х(5 - 3 * 2ˣ - 8 * 4ˣ) - 8(4ˣ - 1) = 0
х(8 * 4ˣ + 3 * 2ˣ - 5) + 8(4ˣ - 1) = 0 цель: разложить на множители...
D=9+160=13²
8 * (2ˣ)² + 3 * 2ˣ - 5 = 8*(2ˣ + 1)*(2ˣ - (5/8)) = (2ˣ + 1)*(8*2ˣ - 5)
x*(2ˣ + 1)*(8*2ˣ - 5) + 8*(2ˣ - 1)(2ˣ + 1) = 0
(2ˣ + 1) * ( x*(8*2ˣ - 5) + 8*(2ˣ - 1) ) = 0
2ˣ + 1 ≠ 0 ни при каких икс... (нет решений...)
8*2ˣ * (х+1) = 5х + 8
2ˣ⁺³ = (5х+8) / (х+1)
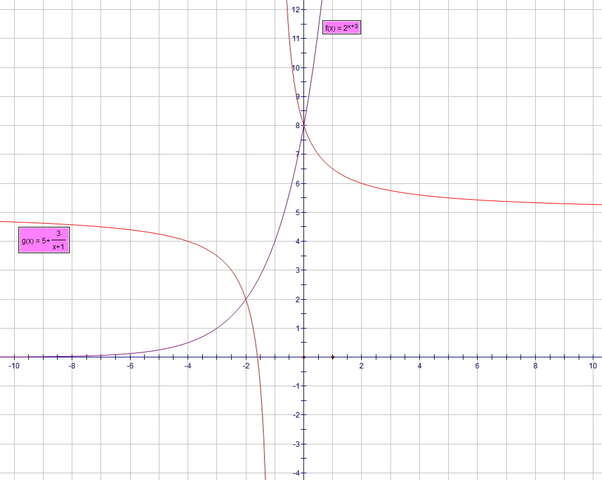
2ˣ⁺³ = 5 + ( 3 / (х+1) ) можно решить графически...
слева: монотонно-возрастающая показательная функция,
справа: гипербола...
два решения: х = -2 и х = 0 (см.график), но х≠0 (см.ОДЗ)
Ответ: х = -2
можно проверить, подставив икс...