2.
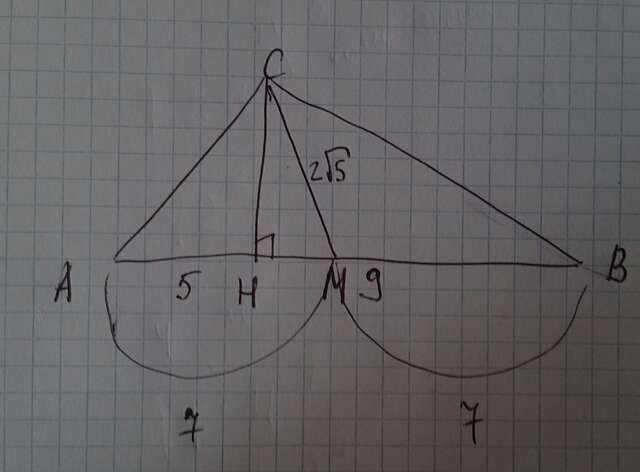
3. Рисунок см. прикрепленную фотографию. Для того, чтобы найти площадь треугольника, надо нужно умножить половину основания на высоту.
Найдем длину основания: AB=AH+MB=5+9=14 см.
Найдем высоту. Сначала найдем расстояние от медианы до высоты, а потом по т. Пифагора найдем высоту. AM=MB=AB/2=7 см
HM=AM-AH=7-5=2см

S=0,5*14*4=28 кв. см.
Ответ:28 квадратных сантиметров.