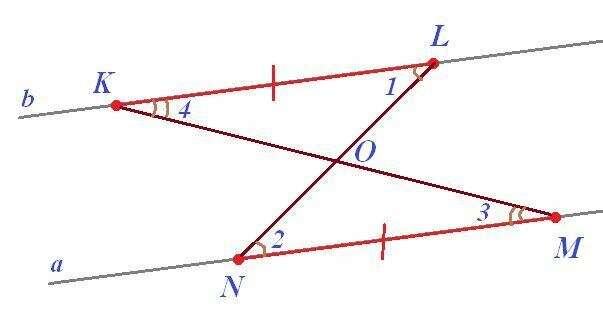
Чертеж - во вложении.
Пусть a||b, KL∈a, NM∈b. Докажем, что OK=OM и OL=ON.
Рассмотрим ΔKOL и ΔMON. У них:
1) KL=NM (по условию)
2) ∠1=∠2 (как накрест лежащие углы при KL||NM и секущей NL)
3) ∠3=∠4 (как накрест лежащие углы при KL||NM и секущей КМ)
Значит, ΔKOL = ΔMON по стороне и прилегающим к ней углам.
Из равенства этих треугольников следует равенство остальных соответствующих элементов этих треугольников. В частности, ОК=ОМ и OL=ON. Доказано.