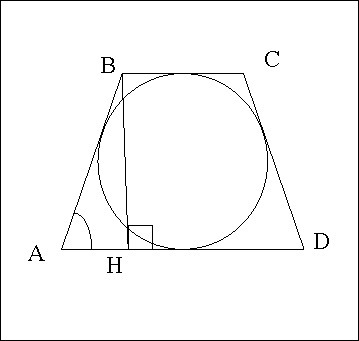
Дано:
АВСD -трапеция, описанная около окружности
АВ=СD - боковые стороны
ВС и АD - основания
S ABCD = 98
Найти Р - периметр ABCD
Решение
1) S ABCD = (ВС+AD)*BH/2
Так как трапеция ABCD описана вокруг окружности, то у неё, как у любого четырёхугольника, описанного около окружности суммы противоположных сторон равны между собой.
ВС + AD = AB+CD.
А так как AB=CD, то ВС+AD=2AB.
Получаем периметр Р
Р = АВ+ВС+СD+AD = 4 AB
Р = 4·АВ
2) Тогда площадь S ABCD = 2АВ*BH/2 = АВ*ВН
S ABCD = АВ*ВН
3) Проведём ВН ┴ AD.
В прямоугольном ∆АВН по условию
ВН = АВ/2
4) Подставим ВН=АВ/2 в формулу площади S ABCD = АВ*ВН и получим:
АВ*АВ/2 = S ABCD
АВ² = 98*2
АВ² = 196
АВ = √196
АВ = 14
5) Наконец, находим периметр Р
Р = 4 AB
Р = 4 * 14 = 56
Ответ: Р = 56