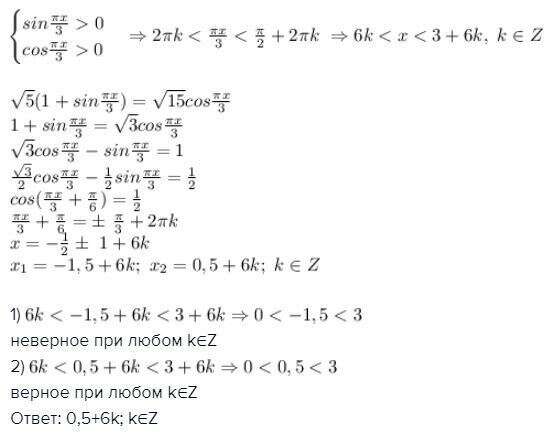0 \\ cos\frac{\pi x}{3} >0 \end {cases} \Rightarrow 2\pi k<\frac{\pi x}{3} <\frac{\pi}{2} + 2\pi k \ \Rightarrow 6k<x<3+6k,\ k \in Z " alt=" \begin {cases} sin\frac{\pi x}{3} >0 \\ cos\frac{\pi x}{3} >0 \end {cases} \Rightarrow 2\pi k<\frac{\pi x}{3} <\frac{\pi}{2} + 2\pi k \ \Rightarrow 6k<x<3+6k,\ k \in Z " align="absmiddle" class="latex-formula">
0 \\ cos\frac{\pi x}{3} >0 \end {cases} \Rightarrow 2\pi k<\frac{\pi x}{3} <\frac{\pi}{2} + 2\pi k \ \Rightarrow 6k<x<3+6k,\ k \in Z " alt=" \begin {cases} sin\frac{\pi x}{3} >0 \\ cos\frac{\pi x}{3} >0 \end {cases} \Rightarrow 2\pi k<\frac{\pi x}{3} <\frac{\pi}{2} + 2\pi k \ \Rightarrow 6k<x<3+6k,\ k \in Z " align="absmiddle" class="latex-formula">

1) 
неверное при любом k∈Z
2) 
верное при любом k∈Z
Ответ: 0,5+6k; k∈Z