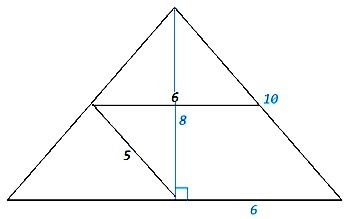
Средняя линия треугольника соединяет середины сторон, параллельна третьей стороне и равна ее половине. Знаем средние линии, следовательно знаем стороны. Основание равно 6*2=12, боковые стороны равны 5*2=10.
Опустим высоту на основание. Высота будет являться медианой и разделит основание пополам, а равнобедренный треугольник - на два прямоугольных. Прямоугольный треугольник c катетом 6 и гипотенузой 10 - египетский (3:4:5), множитель 2, высота равна 4*2=8.
S=12*8/2=48.
ИЛИ
Основание b=12, боковые стороны a=10.
По формуле Герона
S= b/2 *√((a+b/2)(a-b/2)) =6√(16*4) =6*8 =48