Равнобедренный треугольник ABC со сторонами AB=BC=2 sqrt 2 вписан в полукруг так что AC...

Question

Равнобедренный треугольник ABC со сторонами AB=BC=2 sqrt 2 вписан в полукруг так что AC является диаметром этого полукруга . какова площадь двух сегментов заключенных между хордами AB, BC их дугами

Answer 1

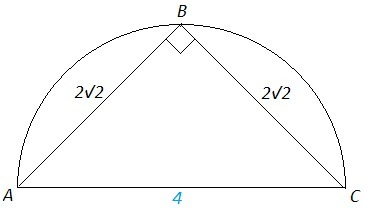
Вписанный угол ABC  - прямой, так как опирается на диаметр.

S(ABC)= 2√2*2√2/2 =4

В равнобедренном прямоугольном треугольнике стороны относятся как 1:1:√2.

AC= 2√2*√2 =4

Sкр= π (AC/2)^2 =4π

Если из площади полукруга вычесть площадь треугольника, получим площадь двух сегментов.

Sкр/2 -S(ABC) =2π-4 =2(π-2) ~2,28

---