По теореме Виета для кубического уравнения ax^3+bx^2+cx+d=0
x1*x2*x3 = -d/a
В нашем случае: x1*x2*x3 = -8/1 = -8.
2 способ.
Будем раскладывать на скобки.
Проверим корень x = 1.
1 - 3 - 6 + 8 = -2-6+8 = -8+8 = 0, всё верно => x = 1 -- корень.
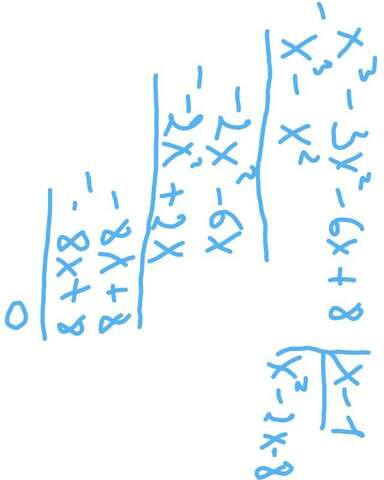
Поделим уравнение на (x-1): см.приложение.
Получаем: (x-1)*(x^2-2x-8) = 0
x^2-2x-8=0
x1 = 4
x2 = -2
x3 = 1
=> 4*(-2)*1 = -8