1 \\ \\ ODZ: \ $\left\{ \begin{gathered} \dfrac{2x-1}{x+2}>0 \\ x + 2\ne 0 \\ \end{gathered} \right.$ \ ; \ $\left\{ \begin{gathered} \dfrac{2(x-\dfrac{1}{2})}{x+2} > 0 \\ x \ne - 2 \\ \end{gathered} \right.$ \ ; \ x \in (-\infty ; -2)\cup (\dfrac{1}{2}; +\infty) " alt=" \log_{\frac{1}{3}}(\dfrac{2x-1}{x+2}) > 1 \\ \\ ODZ: \ $\left\{ \begin{gathered} \dfrac{2x-1}{x+2}>0 \\ x + 2\ne 0 \\ \end{gathered} \right.$ \ ; \ $\left\{ \begin{gathered} \dfrac{2(x-\dfrac{1}{2})}{x+2} > 0 \\ x \ne - 2 \\ \end{gathered} \right.$ \ ; \ x \in (-\infty ; -2)\cup (\dfrac{1}{2}; +\infty) " align="absmiddle" class="latex-formula">
\log_{\frac{1}{3}}(\dfrac{1}{3})^{1} \\ \\ \dfrac{2x-1}{x+2} < \dfrac{1}{3} \\ \\ \dfrac{2x-1}{x+2} - \dfrac{1}{3}< 0 \\ \\ \dfrac{3(2x-1) - 1(x+2)}{3(x+2)} < 0 \\ \\ \dfrac{5x-5}{3(x+2)} < 0 \\ \\ \dfrac{5(x-1)}{3(x+2)} < 0 \ / * \dfrac{3}{5} \\ \\ x \in (-2;1) " alt=" \log_{\frac{1}{3}}(\dfrac{2x-1}{x+2}) >\log_{\frac{1}{3}}(\dfrac{1}{3})^{1} \\ \\ \dfrac{2x-1}{x+2} < \dfrac{1}{3} \\ \\ \dfrac{2x-1}{x+2} - \dfrac{1}{3}< 0 \\ \\ \dfrac{3(2x-1) - 1(x+2)}{3(x+2)} < 0 \\ \\ \dfrac{5x-5}{3(x+2)} < 0 \\ \\ \dfrac{5(x-1)}{3(x+2)} < 0 \ / * \dfrac{3}{5} \\ \\ x \in (-2;1) " align="absmiddle" class="latex-formula">
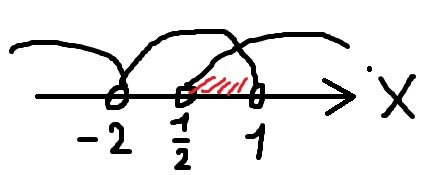
С учётом ОДЗ (1):
Ответ: x ∈ (1/2 ; 1)
Примечание: если основание логарифма относится к промежутку от 0 до 1, то знак неравенства меняется в противоположную сторону.
