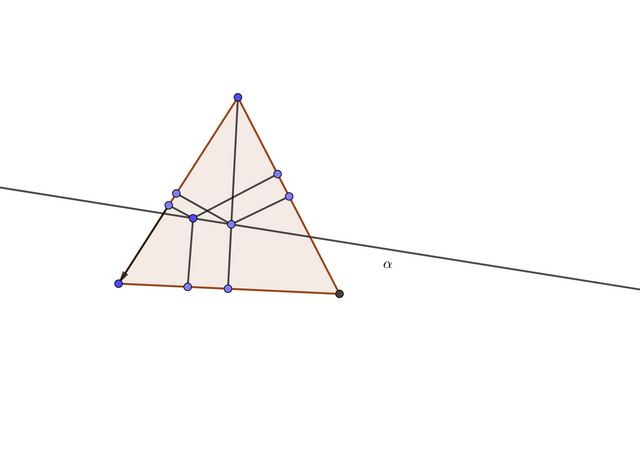
Рассмотрим точку M, которая совпадает с центром вписанной окружности треугольника ABC; Поскольку точки A1, B1, C1 - концы медиан, проведенных к соответствующим сторонам, то все слагаемые в сумме равны, равенство очевидно. Рассмотрим высоту BB1; Точка M лежит на ней. Будем двигать точку М по этой высоте. BC1 и A1B остаются равными уменьшаясь, а AC1 и A1C увеличиваясь, также остаются равными. Отрезки AB1 и B1C остаются равными. Значит равенство сохраняется. Проведем теперь прямую  перпендикулярную высоте BB1; Пусть угол между этой прямой и перпендикуляром, проведенным из точки M (на рис. она посередине) равен β. Заметим, что β=60/2=30°; Пусть сдвиг точки по прямой
перпендикулярную высоте BB1; Пусть угол между этой прямой и перпендикуляром, проведенным из точки M (на рис. она посередине) равен β. Заметим, что β=60/2=30°; Пусть сдвиг точки по прямой  равен x; С одной стороны, одна сумма изменилась на величину -xsinβ - xsinβ + x = -x+x=0; Другая значит тоже изменилась на 0. Итак, сумма осталась постоянной. Мы двигали точку в двух ортогональных направлениях. Используя суперпозицию (наложение движений) приходим к выводу, что равенство выполняется при любом положении точки M
равен x; С одной стороны, одна сумма изменилась на величину -xsinβ - xsinβ + x = -x+x=0; Другая значит тоже изменилась на 0. Итак, сумма осталась постоянной. Мы двигали точку в двух ортогональных направлениях. Используя суперпозицию (наложение движений) приходим к выводу, что равенство выполняется при любом положении точки M