Высоты BP и CQ треугольника ABC пересекаются в точке H. Оказалось, что BH = AC. Найдите...

Question

Высоты BP и CQ треугольника ABC пересекаются в точке H. Оказалось, что BH = AC. Найдите возможные значения угла ABC.

Answer 1

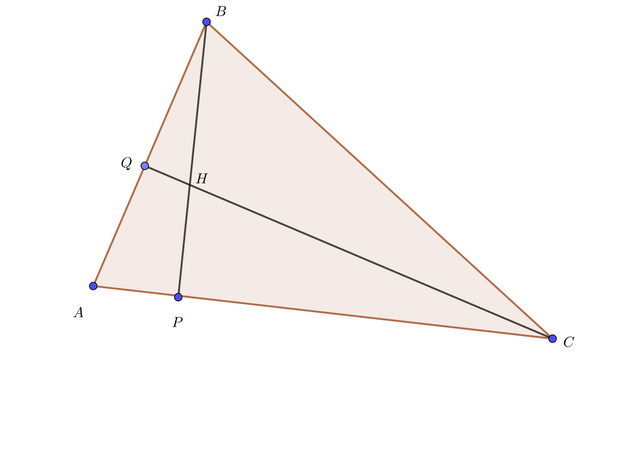
Треугольники BQH и ABP подобны. Также подобны треугольники AQC и ABP; Поэтому треугольники BQH и AQC подобны. При этом BH = AC, значит, эти треугольники равны. Отсюда BQ = QC и ∠ABC = 45°. Случаи с тупоугольным и прямоугольным треугольниками дают те же результаты

---

Comments

Согласен, подобны - общий угол A. Но откуда 45°?

---

там же написано bq=qc

---

Согласен, равны и...? Не понимаю, откуда 45°.

---

bqc - прямоугольный треугольник, в котором равны катеты

---

Смешно получилось. Не увидел очевидного. А если угол ABC тупой?

---

Тогда угол abc 135°

---

А где это в ответе?

---

ну... ну... забыл :(

---

Бывает. У меня немного другое доказательство, я провел ещё одну высоту. QH = AH и т.д.

---

Опечатался: QH = QA и т.д.