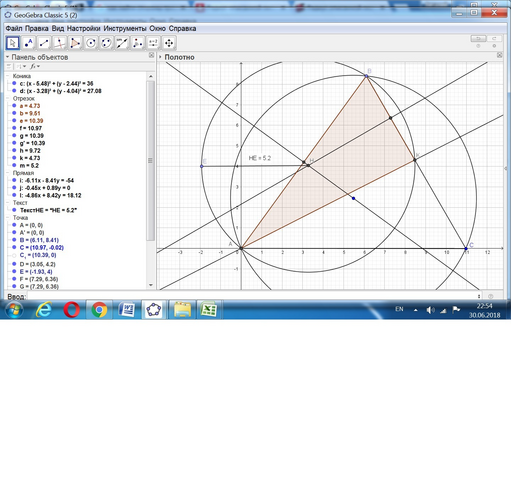
Радиус описанной окружности равен отношению длины стороны треугольника к удвоенному синусу противолежащего этой стороне угла.
Отсюда находим длины сторон треугольника.
a(BC) = 2RsinA = 2*6*sin54° = 12*0,809016994 = 9,708203932.
b(AC) = 2RsinB = 2*6*sin66° = 12*0,913545458 = 10,96254549
.
c(AB) = 2RsinC = 2*6*sin 60° = 12*0,866025404 = 10,39230485
.
Здесь угол С = 180°-54°-66° = 60°.
Находим длину биссектрисы АК = (2bc*cos(A/2))/(b + c) = 9,506871723
.
Биссектриса делит сторону ВС точкой К на отрезки, пропорциональные прилегающим сторонам.
ВК = (ас)/(с -в) = 4,724482409.
KC = BC - BK = 4,983721523
.
Теперь у треугольника АВК известны все стороны.
Площадь его определим по формуле Герона.
S(ABK) = √(p(p-a)(p-b)(p-k)) = 22,42674559
кв.ед.
Здесь a = BK = 4,724482409.
b = AK = 9,506871723
.
k = AB = 10,39230485
.
р = (a+b+k)/2 = 12,3118295
..
Тогда радиус описанной около треугольника АВК окружности равен:
R = (abk)/(4S) = 5,203283414.