1+㏒₃(㏒₃(x+4))>0·························

Question

1+㏒₃(㏒₃(x+4))>0·························

Answer 1

0 \\ \\ ODZ: \ $\left\{ \begin{gathered} x + 4 > 0 \\ \log _{3}(x+4)> 0 \\ \end{gathered} \right.$ \ \ ; \ \ $\left\{ \begin{gathered} x > -4 \\ x > -3 \\ \end{gathered} \right.$ \ \ ; \ \ x \in(-3;+\infty) \\ \\ \log_{3}(\log_{3}(x+4)) > \log_{3}3^{-1} \\ \\ \log_{3}(x+4) > 3^{-1} \\ \\ \log_{3}(x + 4) > \log _{3}3^{\frac{1}{3}} \\ \\ x + 4 > \sqrt[3]{3} \\ \\ x > \sqrt[3]{3} - 4 " alt=" 1 + \log_{3}(\log_{3}(x+4))>0 \\ \\ ODZ: \ $\left\{ \begin{gathered} x + 4 > 0 \\ \log _{3}(x+4)> 0 \\ \end{gathered} \right.$ \ \ ; \ \ $\left\{ \begin{gathered} x > -4 \\ x > -3 \\ \end{gathered} \right.$ \ \ ; \ \ x \in(-3;+\infty) \\ \\ \log_{3}(\log_{3}(x+4)) > \log_{3}3^{-1} \\ \\ \log_{3}(x+4) > 3^{-1} \\ \\ \log_{3}(x + 4) > \log _{3}3^{\frac{1}{3}} \\ \\ x + 4 > \sqrt[3]{3} \\ \\ x > \sqrt[3]{3} - 4 " align="absmiddle" class="latex-formula">

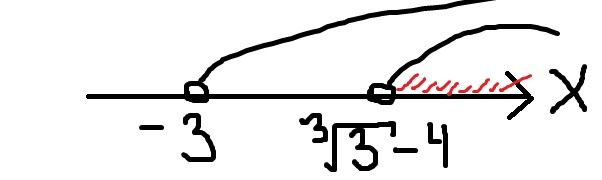
С учётом ОДЗ (1):

Ответ: x ∈ (³√3 - 4 ; +∞ )

---