Перпендикуляр опущений точки перетину діагоналей ромба на його сторону ділить на відрізки...

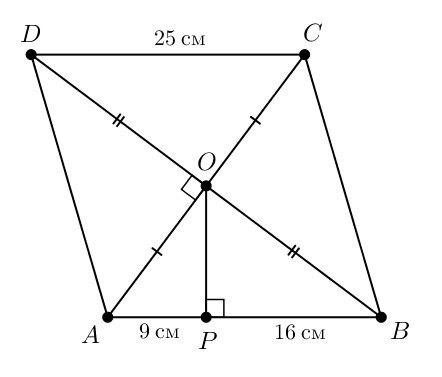
См. рисунок. Диагонали ромба перпендикулярны, поэтому треугольник Δ AOB прямоугольный, а отрезок OP — его высота. Найдём её. Высота прямоугольного треугольника равна среднему геометрическому отрезков, на которые она делит гипотенузу:

$OP= \sqrt{16 \cdot 9}= 4 \cdot 3=12.$

Площадь ромба равна произведению стороны на высоту. Высота ромба в два раза больше высоты Δ AOB (поскольку Δ AOB = Δ ODC по трём сторонам, ведь диагонали в точке O делятся пополам, а высоты равных треугольников равны), поэтому:

$S=(16+9) \cdot 2 \cdot 12=25 \cdot 24=600\\$

Ответ: 600 см².

Перпендикуляр опущений точки перетину діагоналей ромба ** його сторону ділить ** відрізки...

Перпендикуляр опущений точки перетину діагоналей ромба його сторону ділить відрізки...