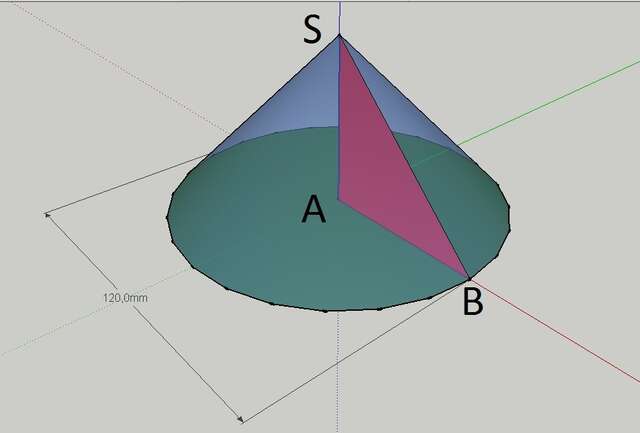
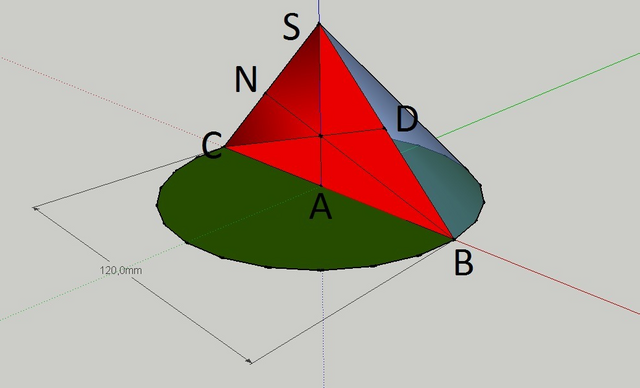
Рассмотрим треугольник АВS, который является частью (половиной) осевого сечения конуса. Сторона АВ явлется радиусом основания конуса. Rк = Dк / 2 = 12см / 2 = 6см; По условию угол ASB = 60°, тогда осевое сечение конуса представляет собой равносторонний треугольник CSB в котором SA - высота, медиана и биссектриса, проведенные из точки S к стороне АВ; CD - высота, медиана и биссектриса, проведенные из точки С к стороне BS; BN - высота, медиана и биссектриса, проведенные из точки В к стороне CS. Отсюда SA = CD = BN = CB √3 / 2 = 12см * 1,73 / 2 = 10,38 см. Rосн = 6см; высота AS = 10,38 см.