Биссектрисы KA и МB треугольника KMP пересекаются в точке O . Определите отношение...

Question

Биссектрисы KA и МB треугольника KMP пересекаются в точке O . Определите отношение KO:OA,если KB=18 дм, BP=12 дм и AP=20 дм

Comments

Такого треугольника быть не может: KB должно быть равно 12, а BP - 18. Но на решение задачи это не влияет. KO/OA=3/2.

---

Поясню. KM/MP = KB/BP = 18/12 = 3/2 = и KM/MA = 3/2. Неувязочка.

Answer 1

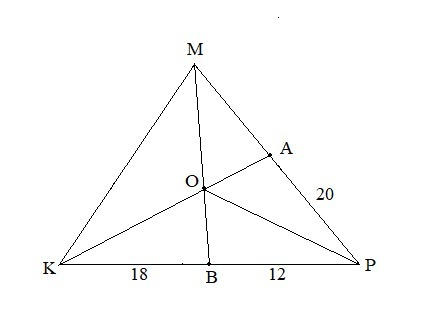
1-й способ.

KP = KB + BP = 18 + 12 = 20 дм

По свойству биссектрисы: KM/MA = KP/AP

В △KMA MO – биссектриса. KM/KO = MA/OA ⟹ KM/MA = KO/OA

Значит, KO/OA = KP/AP = 30/20 = 3/2.

2-й способ.

Биссектрисы пересекаются в одной точке. ⟹ PO – биссектриса,

KP/KO = AP/OA ⟹ KP/AP = KO/OA = 30/20 = 3/2.

---