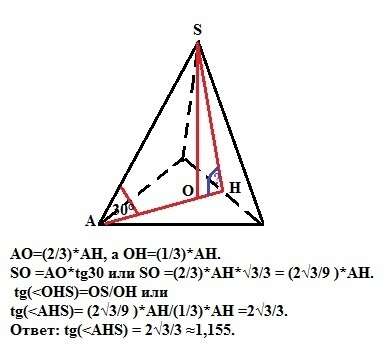
В правильном треугольнике АВС высота АН является и медианой. По свойству медианы АО=(2/3)*АН, а ОН=(1/3)*АН.
В прямоугольном треугольнике ASO угол SAO=30° (дано). Высота пирамиды SO =АО*tg30 или SO =(2/3)*АН*√3/3 = (2√3/9 )*АН.
Угол между плоскостью боковой грани и плоскостью основания - это угол AHS по определению: "Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (АН и SH перпендикулярны ребру ВС двугранного угла ABCS )".
Тогда тангенс искомого угла tg(tg(Ответ: tg( ≈1,155.