Центр координат помещаем в центр окружности. Будем искать закон распределения по оси Х.
Уравнение окружности
x^2+y^2=R^2
y=R√(1-x^2/R^2)
Длина окружности 2πR.
Вероятность попадания на окружность 1.
Плотность распределена равномерно.
f(x)= 2/2π/y - две полуокружности.
f(x) = 1/(πR*√(1-x^2/R^2)) - искомая функция. -R <=x<= R<br>
Проверяем
F'(x) = f(x)
F(-R)= 0
F(x) = arcsin(x/R)/π+1/2
F(R)=1
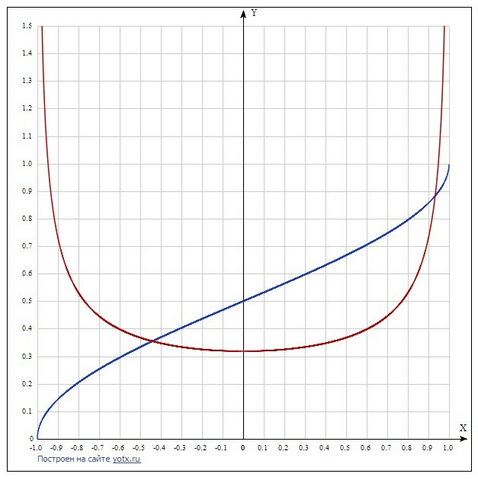
На графике красным f(x)
синим F(x)