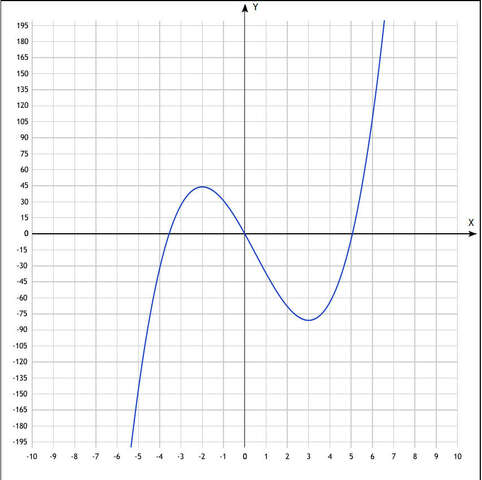
Исследовать функцию на возрастание и экстремум y =2x³ -3x² - 36x
Решение
Найдем производную функции
y' = (2x³ -3x² - 36x)' = (2x³)' - (3x²)' - (36x)' = 6x² - 6x - 36 = 6(x² - x - 6)
Найдем критические точки приравняв производную к нулю y' = 0
x² - x - 6 = 0
D = 1 + 4·6 =
25
x₁ = (1-√(25))/2 = (1 - 5)/2 = -4/2 = -2
x₂ = (1+√(25))/2 = (1 + 5)/2 = 6/2 = 3
Отобразим эти точки на числовой прямой и найдем знаки производной по методу подстановки. Например при х = 0 y'(0) = 6(0² - 0 - 6) =-36<0.<br> + 0 - 0 +
-------------!---------------!--------------------->
-2 3 x
Производная функции положительна и функция возрастает на интервалах x∈(-∞;-2)U(3;+∞)
Производная функции отрицательна и функция убывает на интервале х∈(-2;3)
Функция имеет локальный максимум в точке x = -2
y(-2) = 2·(-2)³-3·(-2)²-36·(-2) = 44
Функция имеет локальный минимум в точке x = 3
y(3) = 2·3³-3·3²-36·3 = -81