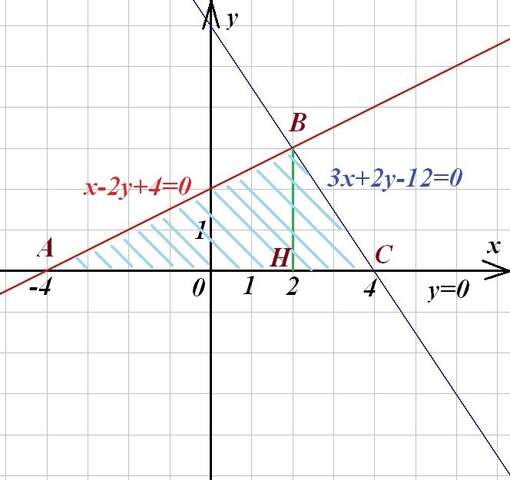
Для построения изображения фигуры выразим у через х:
1) x-2y+4=0 ⇒ у=0,5х+2 - прямая
2) 3x+2y-12=0 ⇒ у=-1,5х+6 - прямая
Найдем абсциссу точки пересечения этих прямых:
0,5х+2=-1,5х+6
2х=4
х=2
Найдем абсциссы точек пересечения каждой прямой с линией у=0:
1) 0,5х+2=0 ⇒ х=-4
2) -1,5х+6=0 ⇒ х=4
Строим линии и красим полученную фигуру (рисунок во вложении).
Вычисляем площадь треугольника АВС:
Ответ: 12
P.S. Как можно заметить по чертежу, площадь треугольника равна половине произведения высоты (равной 3) и стороны (равной 8), т.е. 0,5·3·8=12.