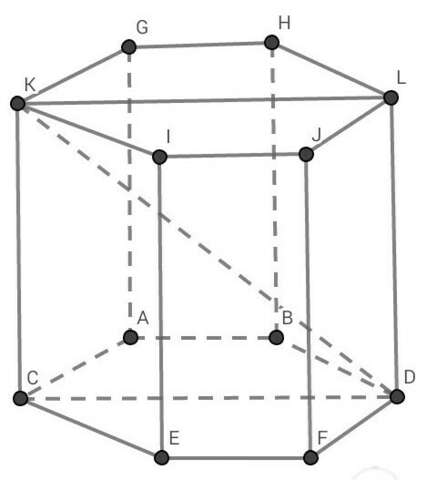
ДАНО: KGHLJICABDFE - правильная шестиугольная призма ; KD = 13 cм ; S бок. пов. = 180 см²
НАЙТИ: S осн.
__________________________
РЕШЕНИЕ:
Пусть сторона основания ( правильного шестиугольника ) равна а , тогда
по свойству шестиугольника его сторона СЕ в два раза меньше его большей диагонали CD => CD = 2a
S бок. пов. = Р осн. × h, где h - высота призмы ( боковое ребро )
180 = 6а × h
h = 180 / 6a = 30 / a
В правильной шестиугольной призме все боковые ребра перпендикулярны основаниям. Значит, ∆ KCD - прямоугольный
По теореме Пифагора:
KD² = KC² + CD²
KC² = KD² - CD²
h² = 13² - ( 2a )²
( 30 / a )² = 13² - ( 2a )²
900 / a² = 169 - 4a²
- 4a⁴ + 169a² = 900
4a⁴ - 169a² + 900 = 0
Пусть а² = t , t > 0 , тогда
4t² - 169t + 900 = 0
D = ( - 169 )² - 4 × 4 × 900 = 28561 - 14400 = 14161 = 119²
t = 6,25
t = 36
Обратная замена:
а² = 6,25
а² = 36
а = 2,5
а = 6
По моему, здесь не достаточно данных, чтобы точно определить площадь основания призмы. Поэтому
Площадь шестиугольника вычисляется по формуле :
S осн. = 3√3 а² / 2 = 3√3 × 6,25 / 2 = 9,375√3
ИЛИ
S осн. = 3√3 × 36 / 2 = 54√3
ОТВЕТ: 9,375√3 или 54√3 см²