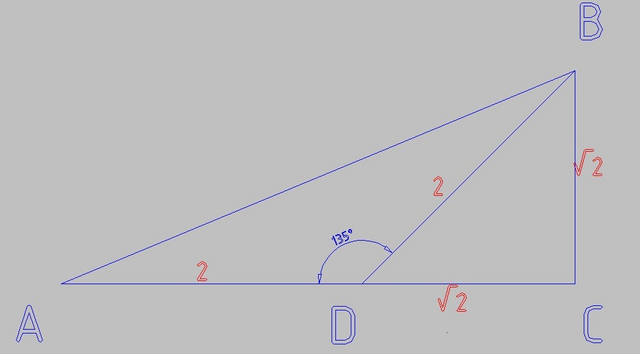
∠CDB = 180 - 135 = 45° как углы, в сумме дающие развёрнутый
∠DBC = 180 - 90 - 45 = 45° т.к. сумма углов ΔBCD равна 180°
и ΔBCD равнобедренный
CD = CB = √2
По теореме Пифагора
DB² = CD² + CB²
DB² = (√2)² + (√2)²
DB² = 2 + 2
DB² = 4
DB = 2
AD = DB = 2
AC = 2 + √2
S(ABC) = 1/2*AC*BC
S(ABC) = 1/2*(2+√2)√2
S(ABC) = 1/2*(2√2 + 2)
S(ABC) = √2 + 1