1. Дано:
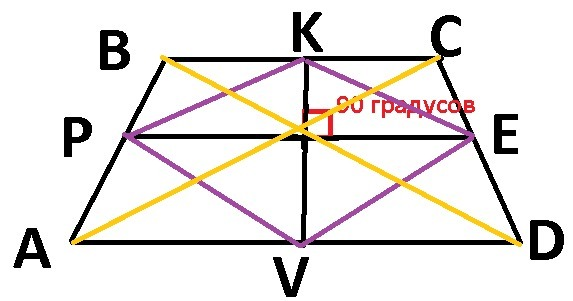
ABCD - трапеция
AD, BC - Основания
K - середина BC
V - середина AD
KV - вторая средняя линия
PE - первая средняя линия
Решение:
Свойство: если в трапеции обе средние линии равны, то её диагонали перпендикулярны, ⇒ угол между диагоналями равен 90°
Доказательство:
KEVP - параллелограмм (Т.к. KE параллельно BD, PV параллельно BD, ⇒ KE параллельно PV. KE = = 1/2 BD, PV = 1/2 BD ⇒ PV = KE. Если в четырёхугольнике две противоположные стороны параллельны и равны, то этот четырёхугольник - параллелограмм).
KV = PE ⇒ это прямоугольник
KE перпендикулярно EV, ⇒ BD перпендикулярно AC
Ответ: 90°