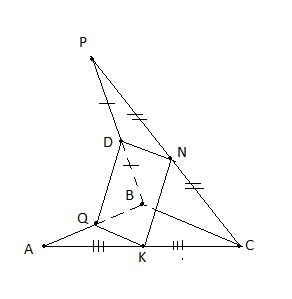
DN
‖ BC как средняя линия △PBC.
Если прямая
a, не лежащая в плоскости α, параллельна некоторой прямой b,
которая лежит в плоскости α, то прямая a параллельна плоскости α.
⟹
плоскость DNK ‖ BC; QK ∈
плоскости ABC
и плоскости DNK
⟹ QK
‖ BC
AK
= KC
⟹ QK
– средняя линия △ABC.
Средняя
линия треугольника, соединяющая середины двух данных сторон, параллельна
третьей стороне и равна ее половине.
⟹
QK = 1/2 BC = 4 см.